DOP Related

We proposed the Variable-Speed Dubins Orienteering Problem and Varying Rewards Dubins Orienteering Problem.

The Dubins Orienteering Problem (DOP) is based on the Orienteering Problem (OP) but considering non-holonomic vehicles. In the DOP we want to compute trajectories for a vehicle with curvature constraints, in which he needs to visit a subset of locations, where each location has a different reward. The objective is to maximize the amount of rewards collected within a given limited budget, being usually time or distance.

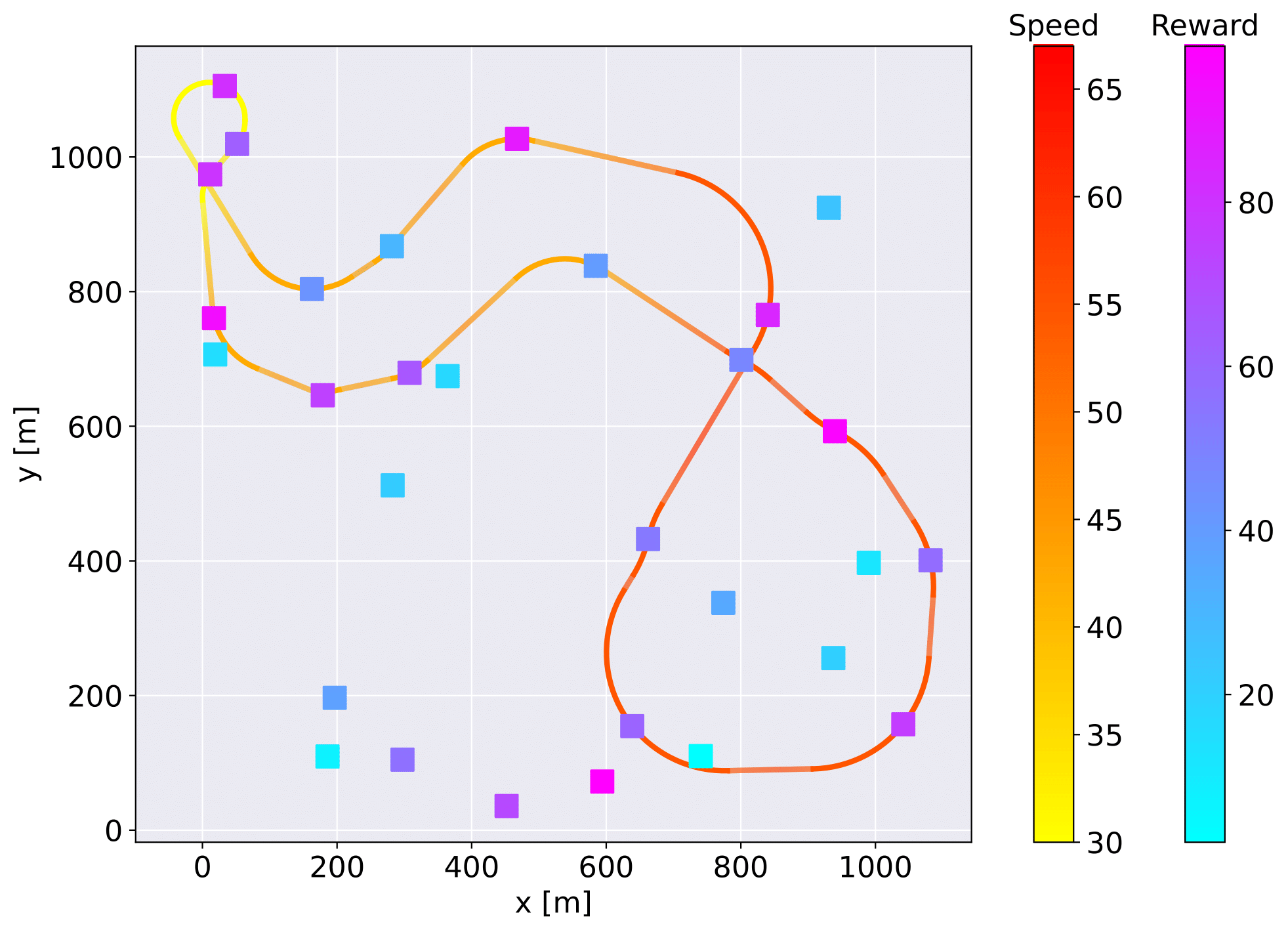
Illustrative example of the best computed trajectory for a VS-DOP instance with 30 vertices. Each vertex is assigned a unique reward, and the trajectory is optimized to vary the vehicle’s velocity to maximize the total rewards collected.

We proposed the Variable-Speed Dubins Orienteering Problem (VS-DOP) where we consider that the vehicle can change its speed during the trajectory, different from the original problem, which considers constant speed. We shown that the VS-DOP outputs better results than compared to the DOP, even if the velocity is maximum at all times.

Our paper about the VS-DOP can be found here.

Currently, we are working on the VS-DOP with rewards that change over time. This means one must consider not only the positions but also the timing of reward collection to maximize the total rewards obtained.